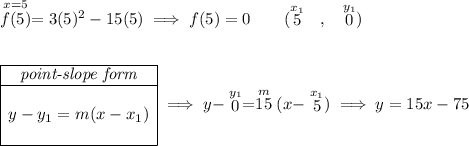at x = 1 we have one tangent line and at x = 5 we have just another tangent line.
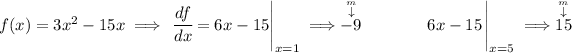
so we have the slopes, but what about the coordinates?
well, for the first one we know x = 1 and we also know f(x), let's use f(1) to get "y", and likewise we'll do the for the second one.
![\stackrel{x=1}{f(1)}=3(1)^2-15(1)\implies f(1)=-12\qquad \qquad (\stackrel{x_1}{1}~~,~~\stackrel{y_1}{-12}) \\\\\\ \begin{array} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-12)}=\stackrel{m}{-9}(x-\stackrel{x_1}{1}) \\\\\\ y+12=-9x+9\implies y=-9x-3 \\\\[-0.35em] ~\dotfill](https://img.qammunity.org/2023/formulas/mathematics/college/o4arn25tq84n5rur77tljcvtyla7b32enz.png)