So, the force that given when the wagon was being pulled is approximately 19.1 N (C).
Introduction
Hi ! For intermesso, this question will adopt a lot about the relationship of impulse to change in momentum. Impulse is the total force applied in a certain time interval. Impulses can cause a change of momentum, because momentum itself is a mass that is affected by the velocity of an object. We know that velocity is a vector quantity easy to change its direction. The relationship between impulse and change in momentum is formulated by :
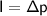
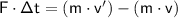
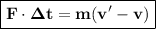
With the following condition :
- I = impulse that given (N.s)
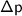 = change of momentum (kg.m/s)
= change of momentum (kg.m/s)- F = force that given (N)
- m = mass of the object (kg)
- v = initial velocity (m/s)
- v' = final velocity (m/s)
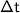 = interval of the time (s)
= interval of the time (s)
Problem Solving
We know that :
- m = mass of the object = 25 kg
- v = initial velocity = 0 m/s
- v' = final velocity = 1.8 m/s
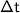 = interval of the time = 2.35 s
= interval of the time = 2.35 s
What was asked :
- F = force that given = ... N
Step by step :
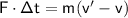
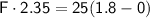


Conclusion
So, the force that given when the wagon was being pulled is approximately 19.1 N (C).