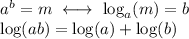Question

I need help with this.

Answer 1

9514 1404 393

Answer:

6/(2+k)

Explanation:

The change of base formula is ...

`\log_a(b)=(\log(b))/(\log(a))`

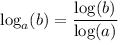
Using this, we can take the logarithm base 2 in the change of base formula for the given expression.

`\log_(20)(64)=(\log_2(64))/(\log_2(20))=(\log_2(2^6))/(\log_2(2^2\cdot5))\\\\=(6)/(\log_2(2^2)+\log_2(5))=\boxed{(6)/(2+k)}`

__

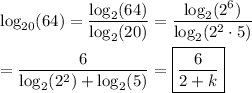
In addition to the change of base formula, the usual rules of logarithms apply.

`a^b=m\ \longleftrightarrow \ \log_a(m)=b\\\log(ab)=\log(a)+\log(b)`