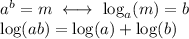9514 1404 393
Answer:
6/(2+k)
Explanation:
The change of base formula is ...
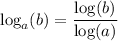
Using this, we can take the logarithm base 2 in the change of base formula for the given expression.

__
In addition to the change of base formula, the usual rules of logarithms apply.