Answer:
The ant has to crawl an approximate distance of 29mm
Explanation:
Given
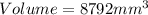
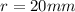 --- radius
--- radius
See attachment
Required
Distance the ant has to crawl (i.e. the slant height)
First, we calculate the height of the hill
The volume of a cone is:
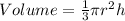
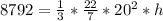
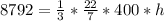
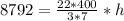
Make h the subject
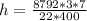
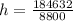
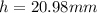
To calculate the slant height (s), we apply Pythagoras theorem
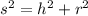
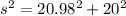
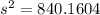
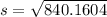
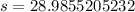
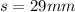 --- approximated
--- approximated