Question

3. How far does the ant crawl to get from the base of the cone to the top of the hill?

Show your work

Write your answer in the space below.

Please helppp

Answer 1

The ant has to crawl an approximate distance of 29mm

Explanation:

Given

`Volume = 8792mm^3`

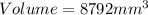
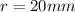`r = 20mm` --- radius

See attachment

Required

Distance the ant has to crawl (i.e. the slant height)

First, we calculate the height of the hill

The volume of a cone is:

`Volume = (1)/(3)\pi r^2h`

`8792 = (1)/(3) * (22)/(7) * 20^2*h`

`8792 = (1)/(3) * (22)/(7) * 400*h`

`8792 = (22* 400)/(3*7) *h`

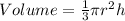
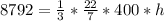
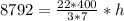
Make h the subject

`h = (8792 * 3 * 7)/(22 * 400)`

`h = (184632)/(8800)`

`h = 20.98mm`

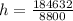
To calculate the slant height (s), we apply Pythagoras theorem

`s^2=h^2 + r^2`

`s^2=20.98^2 +20^2`

`s^2=840.1604`

`s=\sqrt{840.1604`

`s=28.9855205232`

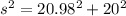
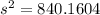
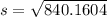
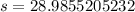
`s= 29mm` --- approximated