Question

g A rigid air cylinder with a volume of 100 cm3 is punctured with a hole having a crosssectional area of 0.3 mm2 . The original pressure and temperature of the air inside the cylinder are 800 kPa and 35 C. As the air leaves the hole in the cylinder, it reaches a pressure of 100 kPa and a temperature of 5 C. The velocity of the air as it escapes through the hole is 100 m/s. Calculate the original mass of air inside the tank and the mass in the tank 5 seconds after it is punctured, assuming the exit conditions of the air remain independent of time g

Answer 1

The volume of the rigid cylinder =
`$100 \ cm^3 = 100 * 10^(-6) \ m^3$`

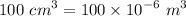
Initial pressure inside the cylinder,
`$P_i = 800 \ kPa$`

Initial temperature inside the cylinder,
`$T_i = 35^\circ C= 308 \ K$`

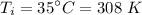
Final temperature inside the cylinder,
`$T_f = 5^\circ C= 278 \ K$`

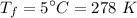
Final pressure inside the cylinder,
`$P_f = 100 \ kPa$`

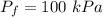
Area of the hole, A =
`$0.3 \ mm^2 = 3 * 10^(-7) \ m^2$`

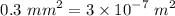
Velocity of the air through the hole, V = 100 m/s

The final pressure and the temperature inside the cylinder will be the condition same as the ambient conditions.

At initial state, from the equation of state,

PV = mRT, where R = 287 J/kg-K for air

`$800 * 10^3 *100 *10^(-6) = m_1 * 287 * 308$`

∴
`$m_1=9.1 * 10^(-4) \ kg$`

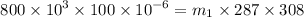
Since the exit condition does not change with time, we have ,

At ambient condition,
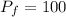`$P_f = 100 \kPa$` and
`$T_f= 278 \ K$`.

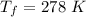Therefore, we can find the density of the air

`$P=\rho R T$`

`$\rho = (P)/(RT)$`

`$=(100 * 10^3)/(287 * 278)$`

`$= 1.25 \ kg/m^3$`

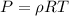
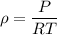
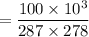
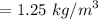
Mass flow rate of air from the cylinder =
`$\dot m$`

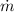
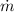`$\dot m$` can be written as
`$\dot m$`
`$=\rho_(f) * A * v$`

`$\dot m$` =
`$1.25 * 3 * 10^(-7) * 100$`

`$\dot m$` =
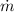
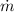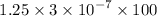
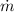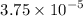`$3.75 * 10^(-5)$` kg/s

Mass escaped from the cylinder in 5 seconds

`$m=3.75 * 10^(-5) * 5$`

`$= 1.875 * 10^(-4) \ kg$`

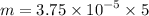
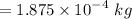
Mass of air remaining in the cylinder after 5 seconds :

`$m_2 = m_1 - m$`

`$m_2 = 9.1 * 10^(-4) - 1.875 * 10^(-4)$`

`$m_2 = 7.225 * 10^(-4) \ kg$`

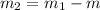
= 0.7225 grams