Question

If
`(dy)/(dx) = cos^(2) ((\pi *y)/(4))` and y = 1 when x = 0, then find the value of x when y = 3.

A. 1/8
B. -π/8
C. -8/π

Answer 1

The ODE

`(\mathrm dy)/(\mathrm dx)=\cos^2\left(\frac{\pi y}4\right)`

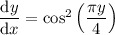
is separable, as

`\frac{\mathrm dy}{\cos^2\left(\frac{\pi y}4\right)}=\mathrm dx`

`\sec^2\left(\frac{\pi y}4\right)\,\mathrm dy=\mathrm dx`

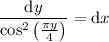
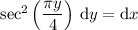
Integrate both sides:

`\displastyle\int\sec^2\left(\frac{\pi y}4\right)\,\mathrm dy=\int\mathrm dx`

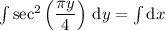
In the left integral, substitute u = πy/4 and du = π/4 dy :

`\displastyle\frac4\pi\int\sec^2(u)\,\mathrm du=\int\mathrm dx`

`\frac4\pi \tan(u)=x+C`

`\frac4\pi\tan\left(\frac{\pi y}4\right)=x+C`

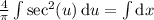
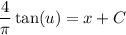
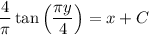
Given that y = 1 when x = 0, we have

`\frac4\pi\tan\left(\frac\pi4\right)=C\implies C=\frac4\pi`

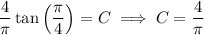
since tan(π/4) = 1. So the ODE has a particular solution of

`\frac4\pi\tan\left(\frac{\pi y}4\right)=x+\frac4\pi`

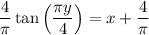
or

`\tan\left(\frac{\pi y}4\right)=\frac{\pi x}4+1`

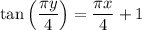
Now when y = 3, we have

`\tan\left(\frac{3\pi}4\right)=\frac{\pi x}4+1`

`-1=\frac{\pi x}4+1`

`-2=\frac{\pi x}4`

`-8=\pi x`

`x=-\frac8\pi`

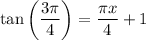
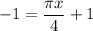
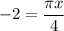
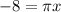
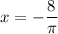
making the answer C.