Question

What is the derivative of secx​

Answer 1

`\displaystyle (d)/(dx)[\sec x] = \sec x \tan x`

General Formulas and Concepts:

Pre-Calculus

• Trigonometric Identities

Calculus

Differentiation

• Derivatives
• Derivative Notation

Basic Power Rule:

1. f(x) = cxⁿ
2. f’(x) = c·nxⁿ⁻¹

Derivative Rule [Quotient Rule]:
`\displaystyle (d)/(dx) [(f(x))/(g(x)) ]=(g(x)f'(x)-g'(x)f(x))/(g^2(x))`

Explanation:

*Note:

This is a known trigonometric derivative.

Step 1: Define

Identify

`\displaystyle y = \sec x`

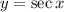
Step 2: Differentiate

1. Rewrite [Trigonometric Identities]:
   `\displaystyle y = (1)/(\cos x)`
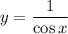
2. Derivative Rule [Quotient Rule]:
   `\displaystyle y' = ((1)' \cos x - 1(\cos x)')/(\cos^2 x)`
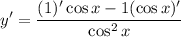
3. Basic Power Rule:
   `\displaystyle y' = ((0) \cos x - 1(\cos x)')/(\cos^2 x)`
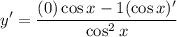
4. Trigonometric Differentiation:
   `\displaystyle y' = ((0) \cos x + 1(\sin x))/(\cos^2 x)`
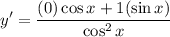
5. Simplify:
   `\displaystyle y' = (\sin x)/(\cos^2 x)`
6. Rewrite:
   `\displaystyle y' = (\sin x)/(\cos x) \cdot (1)/(\cos x)`
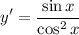
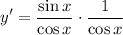
7. Rewrite [Trigonometric Identities]:
   `\displaystyle y' = \tan x \sec x`

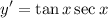
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Differentiation