So, the time needed before you hear the splash is approximately 2.06 s.
Introduction
Hi ! In this question, I will help you. This question uses two principles, namely the time for an object to fall freely and the time for sound to propagate through air. When moving in free fall, the time required can be calculated by the following equation:
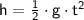

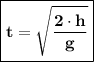
With the following condition :
- t = interval of the time (s)
- h = height or any other displacement at vertical line (m)
- g = acceleration of the gravity (m/s²)
Meanwhile, for sound propagation (without sound reflection), time propagates is the same as the quotient of distance by time. Or it can be formulated by :

With the following condition :
- t = interval of the time (s)
- s = shift or displacement (m)
- v = velocity (m/s)
Problem Solving
We know that :
- h = height or any other displacement at vertical line = 19.6 m
- g = acceleration of the gravity = 9.8 m/s²
- v = velocity = 343 m/s
What was asked :
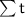 = ... s
= ... s
Step by step :
- Find the time when the object falls freely until it hits the water. Save value as
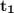
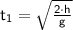
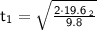
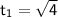

- Find the time when the sound propagate through air. Save value as
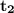
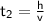
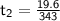
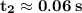
- Find the total time

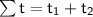

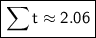
Conclusion
So, the time needed before you hear the splash is approximately 2.06 s.