Question

A soft-drink machine is regulated so that the amount of drink dispensed is approximately normally distributed with known standard deviation, sigma. Given a random sample of n drinks and the sample mean, x-bar, you find a 90% confidence interval for the mean of all drinks dispensed by this machine. Then you calculate a 90% confidence interval (same confidence level) using a larger sample, for example (n 20) drinks. Also, you notice that the sample mean, x-bar, is the same for both samples.

Required:
Was this a reasonable decision?

Answer 1

This is a reasonable decision because the sample size has no effect on the 90% confidence interval

Explanation:

90% confidence interval

larger sample size = 20

condition : sample mean ( x-bar ) is the same for both samples

This is a reasonable decision because the sample size has no effect on the 90% confidence interval

from condition 1 :

Amount of drink dispensed is normally distributed with known standard deviation , given a random sample of n drinks and the sample mean at a confidence interval of 90%

for condition 2 :

sample size = 20

mean = 2.25 ( assumed value )

std = 0.15 ( assumed value )

Z = 1.645 ( Z-value )

determine the 90% confidence interval

= mean ± z
`(std)/(√(n) )`

= 2.25 ± 1.645
`(0.15)/(√(20) )`

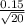
= 2.25 ± 0.0335 = ( 2.2835 , 2.2165 )