Answer:
1) probability that the average concentration of pollutants in the stream on a given day will exceed 85 mg/l is 0.0018
2) probability that a critical level of 95 mg/l will only be exceeded at the most one day in a given week (seven days) is 0.9993
Step-by-step explanation:
Given the data in the question;
mean μ = 50 mg/l
standard deviation σ = 12 mg/l
we know that; x-score = x-μ / σ
1) probability that the average concentration of pollutants in the stream on a given day will exceed 85 mg/l
p( x > 85 ) = P( Z > 85-50 / 12 )
= P( Z > 35/12 )
= P( Z > 2.9166)
= P( Z > 2.92)
= 1 - P( Z > 2.92)
from z-score table; P( Z > 2.92) = 0.9982
= 1 - 0.9982
p( x > 85 ) = 0.0018
Therefore, probability that the average concentration of pollutants in the stream on a given day will exceed 85 mg/l is 0.0018
2) probability that a critical level of 95 mg/l will only be exceeded at the most one day in a given week (seven days). Assume that the pollutant concentrations between days are statistically independent.
p( x > 95 ) = p( Z > 95-50 / 12 )
= p( Z > 45 / 12 )
= p( Z > 3.75 )
= 1 - p( Z > 3.75 )
from z-score table; p( Z > 3.75 ) = 0.9999
= 1 - 0.9999
= 0.0001
Now; p = 0.0001 and n = ( week) = 7
x = number of days × exceeds 99 mg/l
x ¬ Binomial ( n =7 p = 0.0001 )
p(x ≤ 1) = p(x=0) + (p=1)
= ¹∑

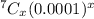
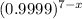
=
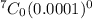
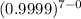
= 7!/(0!(7-0)!)
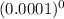
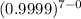
= (1) ( 1 ) ( 0.9993 )
= 0.9993
Therefore, probability that a critical level of 95 mg/l will only be exceeded at the most one day in a given week (seven days) is 0.9993