Question

How many cubes with side lengths of \dfrac13\text{ cm} 3 1 ​ cmstart fraction, 1, divided by, 3, end fraction, start text, space, c, m, end text does it take to fill the prism?

Answer 1

Answer: 48 cubes.

Step-by-step explanation:

V=H*L*W

3*8*2

This equals 48.

Answer 2

48 cubes

Step-by-step explanation:

Given

Cube

`Side\ Length = (1)/(3)cm`

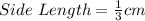
Prism [Missing from the question]

`Length = 1cm`

`Width= 2(2)/(3)cm`

`Height = (2)/(3)cm`

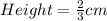
Required

Determine the number of cubes the prism can take

Volume is calculated as:

`V = Length * Width * Height`

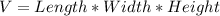
First, calculate the volume of the cube

`V_1 = (1)/(3) * (1)/(3) * (1)/(3) cm^3`

`V_1 = (1)/(27) cm^3`

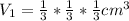
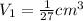
Next, calculate the volume of the prism

`V_2 = 1 * 2(2)/(3) * (2)/(3)\ cm^3`

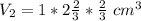
Convert to improper fraction

`V_2 = 1 * (8)/(3) * (2)/(3)\ cm^3`

`V_2 = (16)/(9)\ cm^3`

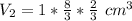
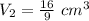
Divide V2 by V1 to get the number of cubes

`Number = (V_2)/(V_1)`

`Number = (16)/(9)/(1)/(27)`

`Number = (16)/(9)*(27)/(1)`

`Number = (16*27)/(9*1)`

`Number = (432)/(9)`

`Number = 48`

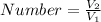
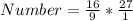
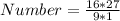
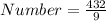
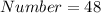
Hence, 48 cubes will fill the prism