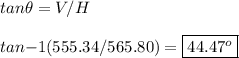Hi there!
We can use a summation of torques to solve.
Recall the following:
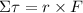
For a system to be static:
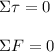
In this case, the counterclockwise torques must sum up to the clockwise torques. We can use the pivot as our fulcrum.
Clockwise torques:
1. Weight of man (F = Mg = 70 · 9.8 = 686 N)
2. Weight of beam (F = Mg = 20 · 9.8 = 196 N)
Counterclockwise torque:
3. VERTICAL comp. of tension (F = Ty = Tsin(φ))
Do a summation of torques. The 'r' value is the distance from the force's line of action to the pivot.
Ex: For the beam, its center of mass (assuming uniform density) is at 1.5 m, or its center.

Now, we can use a summation of forces to determine the vertical and horizontal components of the pivot's force.
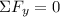
Sum the forces in the vertical direction. Let 'V' represent the pivot's vertical force.
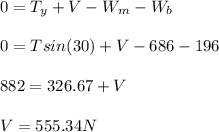
Now, sum the horizontal forces. 'H' is the pivot's horizontal force.
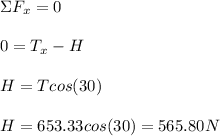
These are the components, so use Pythagorean Theorem to find the total pivot force.
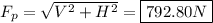
The force will point towards the UPPER LEFT (diagonal). We can solve for the exact angle: