Question

30 POINTS PLS HELP

The slope of the linear function y= 5/4x +1/2 is changed to 5/8 where y= 5/8x + 1/2. Identify the transformation required to produce the new slope, state the equation of the transformed function, ande explainw hat the graph of the tranfsformed line look like.
Here is the picture of the question

Answer 1

We proceed to use the following operations: (i) Vertical translation downwards (
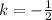`k = -(1)/(2)`), (ii) Vertical compression (
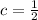`c = (1)/(2)`), (iii) Vertical translation upwards (
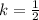`k = (1)/(2)`). The graph is presented below.

Explanation:

To transform
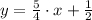`y = (5)/(4)\cdot x + (1)/(2)` into
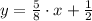`y = (5)/(8)\cdot x + (1)/(2)`, we apply the following steps:

(i) Vertical translation downwards (
`k = -(1)/(2)`)

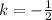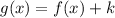`g(x) = f(x) +k` (1)

(ii) Vertical compression (
`c = (1)/(2)`)

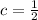`g(x) = c\cdot f(x)` (2)

(iii) Vertical translation upwards (
`k = (1)/(2)`)

`g(x) = f(x) + k`

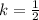Now, we proceed to transform the primitive expression:

Step 1

`f'(x) = (5)/(4)\cdot x`

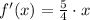
Step 2

`f''(x) = (5)/(8)\cdot x`

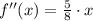
Step 3

`g(x) = (5)/(8)\cdot x + (1)/(2)`

The graph of both function are now presented below. The parent function is the red line and the new function is represented by the blue line.