Answer:
The number of years it will take for the investment to double is approximately 9.1162 years (9 years, 1 month and 12 days)
Step-by-step explanation:
The principal amount the investor deposits in the bank, P = $20,000.00
The annual percentage rate the bank applies to the principal, r = 7.9%
The amount, 'A', in the bank account after a given number of years, 't', is given as follows;
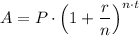
Where;
n = The number of times the interest rate is applied per time period = 1
When the investment (principal amount) doubles, we have;
A = 2·P
r = 0.079
P = $20,000
Plugging in the values into the equation that gives that amount in the account after 't' years, we get;
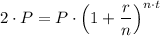
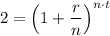

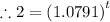
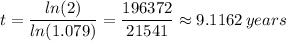
Therefore, it would take t ≈ 9.1162 years for the investment to double