Question

For the given right triangle, find the value x to the nearest tenth:​

Answer 1

Hello!

For this type of problem, we are given a right triangle, and my go-to for finding a side length with another given side length and an angle value would most likely be the law of sines.

The law of sines states that:

`(a)/(sin(A))=(b)/(sin(B))`

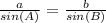
In the given triangle, the
`a` would be 45, and the opposite angle
`71`, would be the
`A`.

The same can be applied to the other side of the proportion.

`x=b`

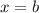
The opposite angle of side
`x` can be found using the definition of the combined angle of a triangle.

`90+71+B=180`

`B=19`

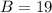
So now we can set up our proportion.

`(45)/(sin(71))=(x)/(sin(19))`

`x=sin(19)*(45)/(sin(71))`

And we get that
`x` is around 15.5.

Hope this helps!