Answer:
a₅₇ = 214
Explanation:
The n th term of an arithmetic sequence is
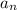 = a₁ + (n - 1)d
= a₁ + (n - 1)d
where a₁ is the first term and d the common difference
Given a₅ = 6 and a₉₂ = 354 , then
a₁ + 4d = 6 → (1)
a₁ + 91d = 354 → (2)
Subtract (1) from (2) term by term to eliminate a₁
0 + 87d = 348
87d = 348 ( divide both sides by 87 )
d = 4
Substitute d = 4 in (1) and solve for a₁
a₁ + 4(4) = 6
a₁ + 16 = 6 ( subtract 16 from both sides )
a₁ = - 10
Then
a₅₇ = - 10 + (56 × 4 ) = - 10 + 224 = 214