Question

Determine the slope intercept form of the linear equation from its graph.​

Answer 1

Given:

The graph of linear function.

To find:

The slope intercept form of the linear equation from the given graph.

Solution:

The slope intercept form of a linear function is:

`y=mx+b`

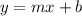
From the given graph it is clear that the graph passes through the points (1,300) and (4,800).

The equation of line is

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

`y-300=(800-300)/(4-1)(x-1)`

`y-300=(500)/(3)(x-1)`

`y-300=(500)/(3)x-(500)/(3)`

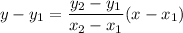
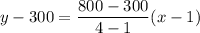
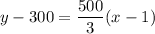
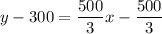
Adding 300 on both sides, we get

`y=(500)/(3)x-(500)/(3)+300`

`y=(500)/(3)x+(900-500)/(3)`

`y=(500)/(3)x+(400)/(3)`

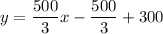
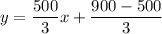
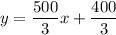
Therefore, the required equation is
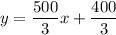`y=(500)/(3)x+(400)/(3)`.