Answer:
x ≈ 49.7°
Explanation:
Since, the given triangle is an isosceles triangle,
Two sides having measure 17 units are equal.
Opposite angles of these equal sides will be equal.
Measure of the third angle = 180° - (x + x)°
By sine rule,
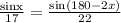
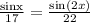 [Since, sin(180 - θ) = sinθ]
[Since, sin(180 - θ) = sinθ]
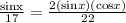
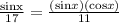
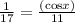
cos(x) =
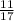
x = 49.68°
x ≈ 49.7°