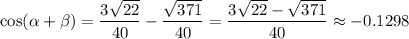Answer:
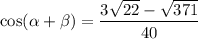
Explanation:
We are given that:

Where both α and β are in QI.
And we want to find cos(α + β).
First, let's determine the side lengths for each angle.
For α, we are given that its cosine is √(11)/8.
And since cosine is the ratio of the adjacent side to the hypotenuse, the adjacent side to α is √11 and the hypotenuse is 8.
Therefore, the opposite side will be:
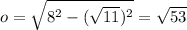
Hence, for α, the adjacent side is √11, the opposite side is √53, and the hypotenuse is 8.
Likewise, for β, we are given that its sine is √7/5.
And since sine is the ratio of the opposite side to the hypotenuse, the adjacent side of β is:
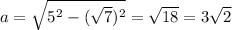
In summary:
For α, the adjacent is √11, the opposite is √53, and the hypotenuse is 8.
For β, the adjacent is 3√2, the opposite is √7, and the hypotenuse is 5.
Using an angle addition identity, we can rewrite our expression as:
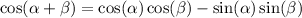
And since both α and β are in QI, all trig ratios will be positive.
Using the above information, we can substitute in the following values:
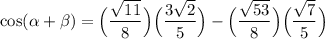
Finally, simplify: