Let's organize our given information.
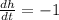
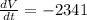
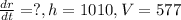
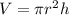
What I'd like to do is solve for
 first, it'll help later.
first, it'll help later.
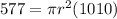
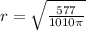
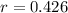
Now, we can differentiate our formula for the volume of a cylinder to find the rate of change of the radius.
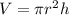
Use the product rule of differentiation.
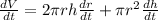
Plug in the information we are given.
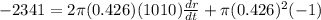
Solve for
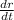 .
.
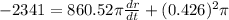
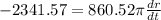
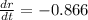
The rate of change of the radius is -0.866 centimeters per minute.
Hope this helps!