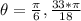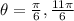Question

Find values of  that satisfy the equation for 0º    360º and 0  θ  2 . Give answers in degrees and radians.

Answer 1

`\theta = 30^\circ, 330^\circ`

`\theta = (\pi)/(6), (11\pi)/(6)`

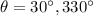
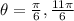
Explanation:

Given [Missing from the question]

Equation:

`cos\theta = (\sqrt 3)/(2)`

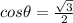
Interval:

`0 \le \theta \le 360`

`0 \le \theta \le 2\pi`

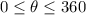
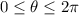
Required

Determine the values of
`\theta`

The given expression:

`cos\theta = (\sqrt 3)/(2)`

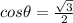
... shows that the value of
`\theta` is positive

The cosine of an angle has positive values in the first and the fourth quadrants.

So, we have:

`cos\theta = (\sqrt 3)/(2)`

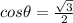
Take arccos of both sides

`\theta = cos^(-1)((\sqrt 3)/(2))`

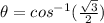
`\theta = 30` --- In the first quadrant

In the fourth quadrant, the value is:

`\theta = 360 -30`

`\theta = 330`

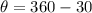
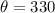
So, the values of
`\theta` in degrees are:

`\theta = 30^\circ, 330^\circ`

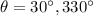
Convert to radians (Multiply both angles by
`\pi/180`)

So, we have:

`\theta = (30 * \pi)/(180), (330 * \pi)/(180)`

`\theta = (\pi)/(6), (33 * \pi)/(18)`

`\theta = (\pi)/(6), (11 * \pi)/(6)`

`\theta = (\pi)/(6), (11\pi)/(6)`