Question

Please help me with both please

Answer 1

1. 3ft
2. 70.529°

Explanation:
Question 1:

Calculated based on 2 given angles and 1 given side.

∠A = 180° - B - C = 0.5236 rad = π/6 = 30°

a = b·sin(A)/sin(B) = 3.4641 = 2
`√(3)`

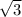
c = b·sin(C)/sin(B) = 6.9282 = 4
`√(3)`

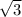
Area =
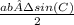`(ab·sin(C))/(2)` = 10.3923

Perimeter p = a + b + c = 16.3923

Semiperimeter s =
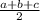`(a + b +c)/(2)` = 8.19615

Height hα =
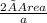`(2×Area)/(a)` = 6

Height hb =
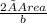`(2×Area)/(b)` = 3.4641

Height hc =
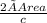`(2×Area)/(c)` = 3

Median ma =
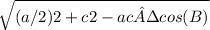`√((a/2)2 + c2 - ac·cos(B))` = 6.245

Median mb =
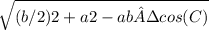`√((b/2)2 + a2 - ab·cos(C))` = 4.58258

Median mc =
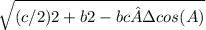`√((c/2)2 + b2 - bc·cos(A))` = 3.4641

Inradius r =
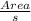`(Area)/(s)` = 1.26795

Circumradius R =
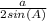`(a)/(2sin(A))` = 3.4641

Question 2:
Calculates b, ∠A, and ∠B based on given c, a, and ∠C.

∠A = arcsin(
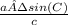`(a·sin(C))/(c)`) = 0.33984 rad = 19.471° = 19°28'16"

∠B = 180° - C - A = 1.23096 rad = 70.529° = 70°31'44"

b =
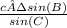`(c·sin(B))/(sin(C)\\)` = 11.31371 = 8√2

Area =
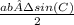`(ab·sin(C))/(2)` = 22.62742

Perimeter p = a + b + c = 27.31371

Semiperimeter s =
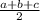`(a + b +c)/(2)` = 13.65685

Height hα =
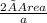`(2×Area)/(a)` = 11.31371

Height hb =
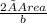`(2×Area)/(b)` = 4

Height hc =
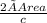`(2×Area)/(c)` = 3.77124

Median ma =
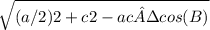`√((a/2)2 + c2 - ac·cos(B) )`= 11.48913

Median mb =
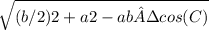`√((b/2)2 + a2 - ab·cos(C))` = 6.9282

Median mc =
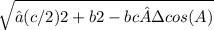`√(√(c/2)2 + b2 - bc·cos(A))` = 6

Inradius r =
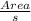`(Area)/(s)` = 1.65685

Circumradius R =
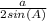`(a)/(2sin(A))` = 6