Answer:
1. 3ft
2. 70.529°
Explanation:
Question 1:
Calculated based on 2 given angles and 1 given side.
∠A = 180° - B - C = 0.5236 rad = π/6 = 30°
a = b·sin(A)/sin(B) = 3.4641 = 2

c = b·sin(C)/sin(B) = 6.9282 = 4

Area =
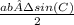 = 10.3923
= 10.3923
Perimeter p = a + b + c = 16.3923
Semiperimeter s =
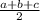 = 8.19615
= 8.19615
Height hα =
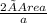 = 6
= 6
Height hb =
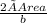 = 3.4641
= 3.4641
Height hc =
 = 3
= 3
Median ma =
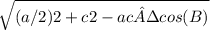 = 6.245
= 6.245
Median mb =
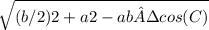 = 4.58258
= 4.58258
Median mc =
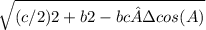 = 3.4641
= 3.4641
Inradius r =
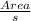 = 1.26795
= 1.26795
Circumradius R =
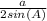 = 3.4641
= 3.4641
Question 2:
Calculates b, ∠A, and ∠B based on given c, a, and ∠C.
∠A = arcsin(
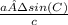 ) = 0.33984 rad = 19.471° = 19°28'16"
) = 0.33984 rad = 19.471° = 19°28'16"
∠B = 180° - C - A = 1.23096 rad = 70.529° = 70°31'44"
b =
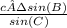 = 11.31371 = 8√2
= 11.31371 = 8√2
Area =
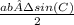 = 22.62742
= 22.62742
Perimeter p = a + b + c = 27.31371
Semiperimeter s =
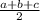 = 13.65685
= 13.65685
Height hα =
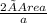 = 11.31371
= 11.31371
Height hb =
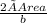 = 4
= 4
Height hc =
 = 3.77124
= 3.77124
Median ma =
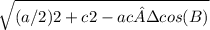 = 11.48913
= 11.48913
Median mb =
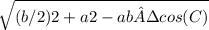 = 6.9282
= 6.9282
Median mc =
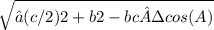 = 6
= 6
Inradius r =
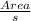 = 1.65685
= 1.65685
Circumradius R =
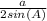 = 6
= 6