Answer:
The dimensions of the field to maximise the area are 100 metres (width) and 200 metres (height).
Explanation:
The formulas for the area (
 ), measured in square metres, and the perimeter (
), measured in square metres, and the perimeter (
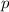 ), measured in metres, of the rectangle are, respectively:
), measured in metres, of the rectangle are, respectively:
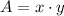 (1)
(1)
 (2)
(2)
Where:
 - Width, measured in metres.
- Width, measured in metres.
 - Height, measured in metres.
- Height, measured in metres.
Note: We assume that height of the rectangle is parallel to the wall of the house.
By (2):
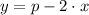
In (1):
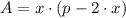
 (3)
(3)
Then, we obtain its first and second derivatives by Differential Calculus:
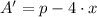 (4)
(4)
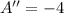 (5)
(5)
By equalising (4) to zero, we find the following critical value for
 :
:
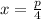
And besides the Second Derivative Test, this solution is associated to an absolute maximum. Given that
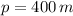 , then the maximum area enclosed by fencing is:
, then the maximum area enclosed by fencing is:
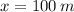
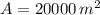
And the height of the triangle is:
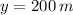
The dimensions of the field to maximise the area are 100 metres (width) and 200 metres (height).