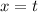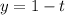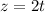Question

Find parametric equations for the tangent line to the curve with the given parametric equations at the specified point. Illustrate by graphing both the curve and the tangent line on a common screen. x=t, y=e^-t, z=2t-t^2; (0, 1, 0)

Answer 1

`x = t`

`y = 1 - t`

`z = 2t`

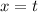
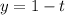
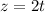
Explanation:

Given

`x=t`

`y=e^(-t)`

`z=2t-t^2`

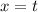
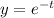
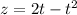
(0, 1, 0)

The vector equation is given as:

`r(t) = (x,y,z)`

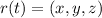
Substitute values for x, y and z

`r(t) = (t,\ e^(-t),\ 2t - t^2)`

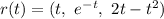
Differentiate:

`r'(t) = (1,\ -e^(-t),\ 2 - 2t)`

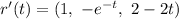
The parametric value that corresponds to (0, 1, 0) is:

`t = 0`

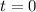
Substitute 0 for t in r'(t)

`r'(t) = (1,\ -e^(-t),\ 2 - 2t)`

`r'(0) = (1,\ -e^(-0),\ 2 - 2*0)`

`r'(0) = (1,\ -1,\ 2 - 0)`

`r'(0) = (1,\ -1,\ 2)`

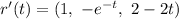
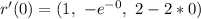
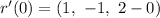
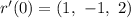
The tangent line passes through (0, 1, 0) and the tangent line is parallel to r'(0)

It should be noted that:

The equation of a line through position vector a and parallel to vector v is given as:

`r(t) = a + tv`

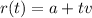
Such that:

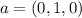`a = (0,1,0)` and
`v = r'(0) = (1,-1,2)`

The equation becomes:

`r(t) = (0,1,0) + t(1,-1,2)`

`r(t) = (0,1,0) + (t,-t,2t)`

`r(t) = (0+t,1-t,0+2t)`

`r(t) = (t,1-t,2t)`

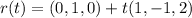
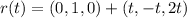
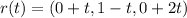
By comparison:

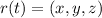`r(t) = (x,y,z)` and
`r(t) = (t,1-t,2t)`

The parametric equations for the tangent line are:

`x = t`

`y = 1 - t`

`z = 2t`