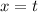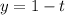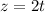Answer:
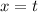
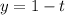
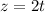
Explanation:
Given
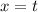
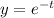
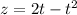
(0, 1, 0)
The vector equation is given as:
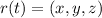
Substitute values for x, y and z
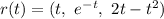
Differentiate:
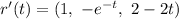
The parametric value that corresponds to (0, 1, 0) is:
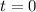
Substitute 0 for t in r'(t)
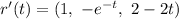
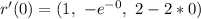
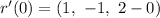
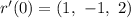
The tangent line passes through (0, 1, 0) and the tangent line is parallel to r'(0)
It should be noted that:
The equation of a line through position vector a and parallel to vector v is given as:
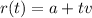
Such that:
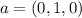 and
and

The equation becomes:
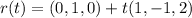
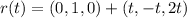
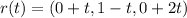

By comparison:
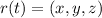 and
and

The parametric equations for the tangent line are: