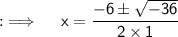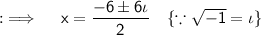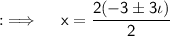We are provided with a quadratic equation , and we have to find it's roots , but let's recall some things
- The Standard Form of a quadratic equation is ax² + bx + c = 0
- If D > 0 , then the equation have two real and distinct roots/zeroes .
- If D = 0 , then the equation have two equal roots/zeroes .
- If D < 0 , then the equation have two imaginary roots/zeroes or you can say that no real roots
Where , D is the Discriminant whose value is b²- 4ac and the roots of the equation are given by a very famous formula called The Quadratic Formula , which is as follows ;
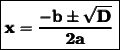
Now , coming back on the question ;
We are provided with the equation x² + 6x = -18 , so on comparing this equation with the standard form of quadratic equation , we have , a = 1 , b = 6 and c = 18 . Now calculating the Discriminant ;
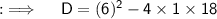
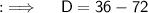
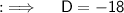
As , D < 0 , so two imaginary roots exist . Now by quadratic formula ;