We are given the slope of the line and a point that it passes through, so we can use the Point-Slope formula:
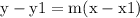
Where
y1 is the y-coordinate of the point, m is the slope and x1 is the x-coordinate.
In this case:
y1=0
m=10
x1=0
Plug in the values:
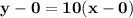
Solve:
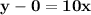

Now, how to graph the line?
Let's look at its equation.
First of all, it has a y-intercept of 0, which means the line touches the y-axis at (0,0)
Now, what about the slope? The slope is 10.
Thus
We move "up 10, over 1, up 10, over 1" and so on, until we have a line.
Then all we have to do is take a ruler and connect the points.
Hope it helps!
~Just a determined gal
#HaveAGreatDay