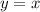Answer:
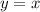
Explanation:
Given
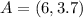

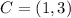
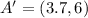
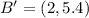

Required
The equation for the line of reflection
Taking points A and A' as a point of reference:
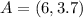 and
and
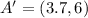
First, calculate the midpoint (M)
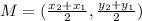

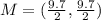
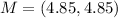
Calculate the slope (m)



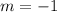
The midpoint of a reflection is always perpendicular to the points being reflected.
So, the slope of
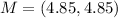 is:
is:

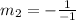
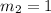
The equation is then calculated as:
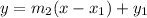
Where:
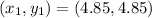
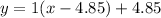
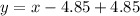
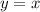
Hence, the equation of line of reflection is: