Answer:
Option A, Left by 4 units
Explanation:
Step 1: Convert g(x) to a function square
We currently have g(x) in this order:

However, we want g(x) to be in this order:

The first thing we have to do is to factor it out:

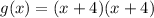
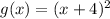
Step 2: Now we can see which way we need to move it
The original form is:

Since the - has changed to a +, that means that we moved -4 spaces down the x-axis. This means that we move left by 4 units.
Answer: Option A, Left by 4 units
Look at the graphs below to make sure: