Explanation:
An exterior angle of a polygon is an angle outside a polygon formed by one of its sides and the extension of an adjacent side. As shown in the figure below, for example, illustrates the exterior angles (red) of a regular convex pentagon (5-sided polygon).
The exterior angle sum theorem states that if a polygon is convex, the sum of its exterior angle will always be 360°. Therefore, the magnitude of each exterior angle of a n-sided polygon can be evaluated using the formula
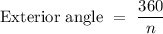 .
.
Hence, for a convex 21 sided-polygon (henicosagon), each exterior angle will be
 .
.
which sum is
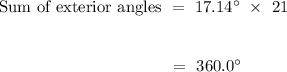 ,
,
agrees with the theorem mentioned above.