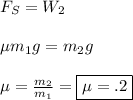Question

Two blocks are connected by a pulley system represented in the diagram below. M1= 60kg and M2=12kg. Wh

is the coefficient of friction required to keep the masses at rest?

Answer 1

Hi there!

Assuming the pulley is frictionless and massless, we can do a summation of forces for each block.

Block 1 has the tension force (in direction of acceleration) and force of static friction acting on it. For the block to be stationary, the net force must be 0, so:

`\Sigma F = T - F_S`

`0 = T - F_S\\\\T = F_S`

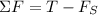
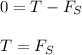
Now, we can do a summation for Block 2.

`\Sigma F = W_2 - T\\\\0 = W_2 - T\\\\T = W_2`

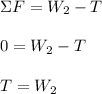
We can substitute this tension in the above equation to solve for the force of static friction and the coefficient of static friction.

`F_S = W_2\\\\\mu m_1g = m_2g\\\\\mu = (m_2)/(m_1) = \boxed{\mu = .2}`