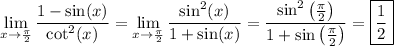Question

Lim x→π/2 1-sinx/cot^2x
any genious help please ​

Answer 1

Rewrite the limand as

(1 - sin(x)) / cot²(x) = (1 - sin(x)) / (cos²(x) / sin²(x))

… = ((1 - sin(x)) sin²(x)) / cos²(x)

Recall the Pythagorean identity,

sin²(x) + cos²(x) = 1

Then

(1 - sin(x)) / cot²(x) = ((1 - sin(x)) sin²(x)) / (1 - sin²(x))

Factorize the denominator; it's a difference of squares, so

1 - sin²(x) = (1 - sin(x)) (1 + sin(x))

Cancel the common factor of 1 - sin(x) in the numerator and denominator:

(1 - sin(x)) / cot²(x) = sin²(x) / (1 + sin(x))

Now the limand is continuous at x = π/2, so

`\displaystyle\lim_(x\to\frac\pi2)(1-\sin(x))/(\cot^2(x))=\lim_(x\to\frac\pi2)(\sin^2(x))/(1+\sin(x))=(\sin^2\left(\frac\pi2\right))/(1+\sin\left(\frac\pi2\right))=\boxed{\frac12}`