Given:
The center of the circle is at (0,0).
The circle passes through the point A(4,-3).
To find:
The radius and the equation of the circle.
Solution:
Distance formula:
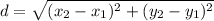
The radius of the circle is the distance between the points (0,0) and (4,-3).
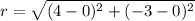
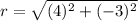
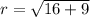
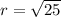
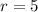
So, the radius of the circle is 5 units.
The standard form of a circle is

Where, (h,k) is center of circle and r is the radius.
Putting h=0, k=0, r=5, we get
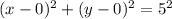
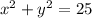
Therefore, the radius of the circle is 5 units and the equation of the circle is
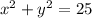 .
.