Answer: y=29 / (4,29)
Explanation:
By graphing
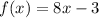 and
and
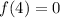 on Desmos. You'll be able to find that when x is 4, y is 29.
on Desmos. You'll be able to find that when x is 4, y is 29.
Similarly, you can plugin 4 into the original equation (
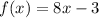 ) Which looks like:
) Which looks like:
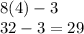
Additionally, you can change
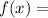 to
to
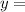 as it is the exact same thing. With that in mind, you can do the same with
as it is the exact same thing. With that in mind, you can do the same with
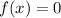 and just change it to x=4. As you're wanting to know what the y-value is when x=4.
and just change it to x=4. As you're wanting to know what the y-value is when x=4.