Answer:
Probability drawing at least one ace of hearts is 3.8 %
Step-by-step explanation:
Probability of drawing at least one ace of hearts = 1 - probability of no aces of hearts being drawn.
Probability of drawing no aces of hearts
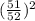
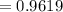
Probability drawing at least one ace of hearts
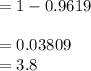 %
%