Answer:
The sum of the area of the shaded regions = 0.248685
Step-by-step explanation:
The sum of the area of the shaded region is given as follows;
The point of intersection of the graphs are;
y = x/2
y = sin²x
∴ At the intersection, x/2 = sin²x
sinx = √(x/2)
Using Microsoft Excel, or Wolfram Alpha, we have that the possible solutions to the above equation are;
x = 0, x ≈ 0.55 or x ≈ 1.85
The area under the line y = x/2, between the points x = 0 and x ≈ 0.55, A₁, is given as follows
1/2 × (0.55)×0.55/2 ≈ 0.075625
The area under the line y = sin²x, between the points x = 0 and x ≈ 0.55, A₂, is given using as follows;
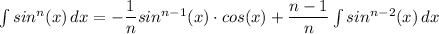
Therefore;
![A_2 = \int\limits^(0.55)_0 {sin^2x} \, dx = (1)/(2) \left [x -sin(x) \cdot cos(x) \right]_0 ^(0.55)](https://img.qammunity.org/2022/formulas/advanced-placement-ap/high-school/9i6ntk3fafhu817wpfiaia9lnqhgq0oy19.png)
∴ A₂ =1/2 × ((0.55 - sin(0.55)×cos(0.55)) - (0 - sin(0)×cos(0)) ≈ 0.0522
The shaded area,
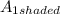 = A₁ - A₂ = 0.075625 - 0.0522 ≈ 0.023425
= A₁ - A₂ = 0.075625 - 0.0522 ≈ 0.023425
Similarly, we have, between points 0.55 and 1.85
A₃ = 1/2 × (1.85 - 0.55) × 1/2 × (1.85 - 0.55) + (1.85 - 0.55) × 0.55/2 = 0.78
For y = sin²x, we have;
![A_4 = \int\limits^(1.85)_(0.55) {sin^2x} \, dx = (1)/(2) \left [x -sin(x) \cdot cos(x) \right]_(0.55) ^(1.85) \approx 1.00526](https://img.qammunity.org/2022/formulas/advanced-placement-ap/high-school/3h5f2nmczq2ocxiw2dkhwl5590913e2x4l.png)
The shaded area,
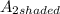 = A₄ - A₃ = 1.00526 - 0.78 ≈ 0.22526
= A₄ - A₃ = 1.00526 - 0.78 ≈ 0.22526
The sum of the area of the shaded regions, ∑A =
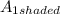 +
+
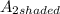
∴ A = 0.023425 + 0.22526 = 0.248685
The sum of the area of the shaded regions, ∑A = 0.248685