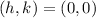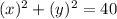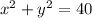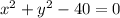Answer:
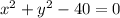
Explanation:
Given
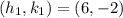
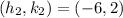
Required
Determine the equation of the circle
First, calculate the midpoint of the given coordinates:
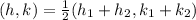
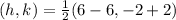
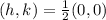
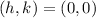
Next, calculate the radius.
This is the distance between
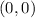 calculated above and any of
calculated above and any of
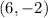
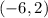
Using:
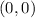 and
and
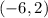 , the radius is:
, the radius is:
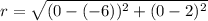
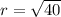
The equation is then calculated using:
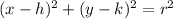
Where:
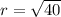 and
and