A sequence of transformations that maps triangle ΔABC to a similar triangle is: D.
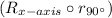 .
.
In Mathematics and Geometry, a reflection over the x-axis can be represented by the following transformation rule (x, y) → (x, -y).
Assuming triangle ABC has the cordinates A (2, 4) and B (2, 5) and we apply a reflection over the x-axis, the coordinates of its image;
(x, y) → (x', -y')
A (2, 4) → A' (2, -4)
B (2, 5) → B' (2, -5)
In Euclidean Geometry, the rotation of a point 90° about the origin in a counterclockwise (anticlockwise) direction would produce a point that has these coordinates (-y, x).
By applying a rotation of 90° counterclockwise about the origin to the new vertices, the coordinates of the image are as follows:
(x, y) → (-y, x)
A' (2, -4) → (-(-4), 2) = A" (4, 2)
B' (2, -5) → (-(-5), 3) = B" (5, 2)
Next, we would determine the length of each sides;
AB = |4 - 5| = 1 unit.
A"B" = |5 - 4| = 1 unit.
Therefore, the corresponding side lengths are equal.