Question

1 Factor the polynomial over the set of real numbers. (a) f(x) = 25x^2 - 10x - 24​

Answer 1

(5x+4)(5x-6)

Explanation:

`25x^(2) -10x-24`

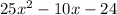
Separate into two parts, first realizing that the only two factor pairs for 25 are 5 and 5 or 1 and 25. Using 5 and 5 makes the most sense, so

(5x )(5x )

The other two numbers need to multiply to -24 and add up to -10.

Pairs that muliply to 24 could be 1 and 24, 2 and 12, 3 and 8, and 4 and 6. The more you factor the easier it will be to quickly discern which numbers to use. In this case, the right pair is 4 and 6. Because it needs to add up to -10, it should be 4 and -6 (because multiplying out, -30 + 20 = -10).

Thus, the final factored equation is (5x+4)(5x-6). You can check this by FOILing and making sure you get the original equation.

Answer 2

The polynomial
`\( f(x) = 25x^2 - 10x - 24 \)` can be factored over the set of real numbers as
`\( f(x) = (25x - 6)(x - 4) \).`

To factor the quadratic polynomial
`\(f(x) = 25x^2 - 10x - 24\)` over the set of real numbers, we can use the factoring methods, such as factoring by grouping or applying the quadratic formula. In this case, factoring by grouping is a suitable approach.

The expression
`\(25x^2 - 10x - 24\)` can be factored by splitting the middle term (-10x) into two terms whose coefficients multiply to give the product of the leading coefficient (25) and the constant term (-24), and then grouping the terms:

`\[ f(x) = 25x^2 - 6x - 4x - 24 \]`

Now, factor by grouping:

`\[ f(x) = (25x^2 - 6x) + (-4x - 24) \]`

`\[ f(x) = x(25x - 6) - 4(25x - 6) \]`

Now, notice that we have a common factor of (25x - 6):

`\[ f(x) = (25x - 6)(x - 4) \]`

Therefore, the polynomial
`\( f(x) = 25x^2 - 10x - 24 \)` can be factored over the set of real numbers as
`\( f(x) = (25x - 6)(x - 4) \).`