Question

A 130 g sample of brass at 120.0 degrees Celsius is placed in a calorimeter cup that contains

130 g of water at 35.0 degrees Celsius. Disregard the absorption of heat by the cup and
calculate the final temperature of the brass and water. Specific heat of water = 4.18 J/gC,
specific heat of brass=0.380 J/gC. Attach your complete solution

Answer 1

`T_(EQ)=42.1\°C`

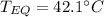
Step-by-step explanation:

Hello there!

In this case, since we are looking for an equilibrium temperature, we can evidence how the net heat flow is 0 as all the heat released by the hot brass is absorbed by the water:

`Q_(brass)+Q_(water)=0`

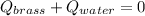
Thus, by writing that equation in terms of mass, specific heat and temperature we obtain:

`m_(brass)C_(brass)(T_(EQ)-T_(brass))+m_(water)C_(water)(T_(EQ)-T_(water))=0`

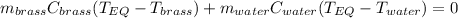
Thus, by applying the following algebra, it is possible to arrive to a clean expression to obtain the equilibrium temperature:

`m_(brass)C_(brass)T_(EQ)+m_(water)C_(water)T_(EQ)=m_(water)C_(water)T_(water)+m_(brass)C_(brass)T_(brass)\\\\T_(EQ)(m_(brass)C_(brass)+m_(water)C_(water))=m_(water)C_(water)T_(water)+m_(brass)C_(brass)T_(brass)\\\\T_(EQ)=}(m_(water)C_(water)T_(water)+m_(brass)C_(brass)T_(brass))/(m_(brass)C_(brass)+m_(water)C_(water))`

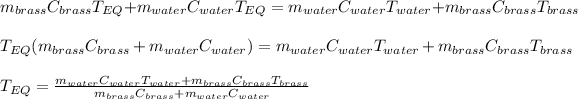
Then, by plugging the masses, specific heats and initial temperatures in, we obtain:

`T_(EQ)=(130g*4.184(J)/(g*\°C) *35.0\°C+130g*0.380(J)/(g*\°C)*120.0\°C)/(130g*4.184(J)/(g*\°C) +130g*0.380(J)/(g*\°C))\\\\T_(EQ)=42.1\°C`

Best regards!