Answer:
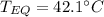
Step-by-step explanation:
Hello there!
In this case, since we are looking for an equilibrium temperature, we can evidence how the net heat flow is 0 as all the heat released by the hot brass is absorbed by the water:
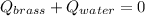
Thus, by writing that equation in terms of mass, specific heat and temperature we obtain:
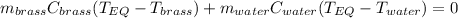
Thus, by applying the following algebra, it is possible to arrive to a clean expression to obtain the equilibrium temperature:
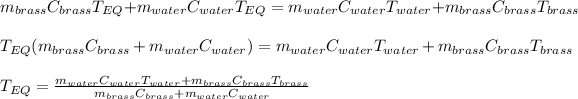
Then, by plugging the masses, specific heats and initial temperatures in, we obtain:
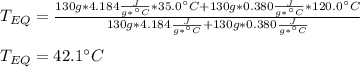
Best regards!