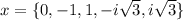Answer:
Explanation:
We are given the function:
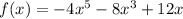
And we want to finds its zeros.
Therefore:

Firstly, we can divide everything by -4:
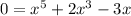
Factor out an x:
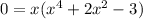
This is in quadratic form. For simplicity, we can let:

Then by substitution:
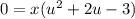
Factor:

Substitute back:
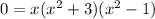
By the Zero Product Property:
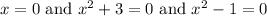
Solving for each case:
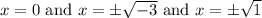
Therefore, our real and complex zeros are: