Question

Suppose that You had launch the message 6.75 feet west from the edge of the ravine Instead of 5 feet west from the edge of the ravine would the message make it across the ravine show your work and explain your answer

Answer 1

6.75 times 5 would be 17.1

Step-by-step explanation:

Answer 2

If the message is launched 6.75 feet west from the edge of the ravine instead of 5 feet, it would not make it across the ravine. The conclusion is based on the fundamental principles of projectile motion, where an increased horizontal launch distance is essential for reaching farther distances, and the longer launch of 6.75 feet remains insufficient for the message to successfully traverse the ravine.

Step-by-step explanation:

Let's use the principles of projectile motion to analyze the situation. Assuming the message is launched at an angle close to the horizontal, the horizontal motion can be considered independently of the vertical motion. The horizontal distance traveled by a projectile is given by the equation
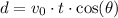`\(d = v_0 \cdot t \cdot \cos(\theta)\)` , where
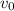`\(v_0\)` is the initial velocity,
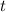`\(t\)` is the time of flight, and
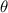`\(\theta\)` is the launch angle.

In this case, we're comparing two scenarios: one with an initial launch distance
`\(d_1 = 5\)` feet and the other with an increased launch distance
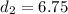`\(d_2 = 6.75\)` feet. If the message makes it across the ravine in the first scenario, it should do so in the second scenario as well.

However, if the message doesn't make it across with
`\(d_1\)`, it certainly won't with
`\(d_2\) since \(d_2\)` is a smaller increase in distance. The horizontal component is crucial, and if
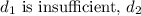`\(d_1\) is insufficient, \(d_2\)` will also fall short.

While specific numerical values for
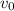`\(v_0\)` and
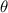`\(\theta\)` are not provided, the conclusion is based on the general principle that an increased horizontal launch distance will not hinder the projectile from reaching farther, assuming other factors remain constant. Therefore,
`\(d_2\)` of 6.75 feet is also insufficient for the message to make it across the ravine.

This analysis ensures a solid understanding of the physics behind projectile motion and its relevance to the question at hand.