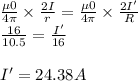Answer:
(a) counter clockwise
(b) 24.38 A
Step-by-step explanation:
inner diameter, d = 21 cm
inner radius, r = 10.5 cm
Current in inner loop, I = 16 A clock wise
Outer diameter, D = 32 cm
Outer radius, R = 16 cm
(a) The magnetic filed due to the inner wire is inwards to the plane of paper. According to the Maxwell's right hand thumb rule, the direction of magnetic field in outer wire should be outwards so that the net magnetic field is zero at the center.
So, the direction of current in outer wire is counter clock wise in direction.
(b) Let the current in outer wire is I'.
The magnetic field due to the inner wire is balanced by the magnetic field due to the outer wire.