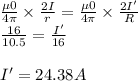Question

Two round concentric metal wires lie on a tabletop, one inside the other. The inner wire has a diameter of 21.0 cm and carries a clockwise current of 16.0 A , as viewed from above, and the outer wire has a diameter of 32.0 cm.

Required:
a. What must be the direction (as viewed from above) of the current in the outer wire so that the net magnetic field due to this combination of wires is zero at the common center of the wires?
b. What must be the magnitude of the current in the outer wire so that the net magnetic field due to this combination of wires is zero at the common center of the wires?

Answer 1

(a) counter clockwise

(b) 24.38 A

Step-by-step explanation:

inner diameter, d = 21 cm

inner radius, r = 10.5 cm

Current in inner loop, I = 16 A clock wise

Outer diameter, D = 32 cm

Outer radius, R = 16 cm

(a) The magnetic filed due to the inner wire is inwards to the plane of paper. According to the Maxwell's right hand thumb rule, the direction of magnetic field in outer wire should be outwards so that the net magnetic field is zero at the center.

So, the direction of current in outer wire is counter clock wise in direction.

(b) Let the current in outer wire is I'.

The magnetic field due to the inner wire is balanced by the magnetic field due to the outer wire.

`( \mu 0)/(4\pi)* (2 I)/(r)=(\mu 0)/(4\pi)* (2 I')/(R)\\(16)/(10.5)=(I')/(16)\\\\I' = 24.38 A`

Answer 2

a). B at the center :

`$=(u* I)/(2R)$`

Here, one of the current is in the clockwise direction and therefore, the other current must be in the clockwise direction in order to cancel out the effect of the magnetic field that is produced by the other.

Therefore, the answer is ANTICLOCKWISE or COUNTERCLOCKWISE

b). Also, the sum of the fields must be zero.

Therefore,

`$\left((u* I_1)/(2R_1)\right) + \left((u* I_2)/(2R_2)\right) = 0$`

So,

`$(I_1)/(d_1)= (I_2)/(d_2)$`

`$=(16)/(21)=(I_2)/(32)$`

`$I_2=24.38 $` A

Therefore, the current in the outer wire is 24.38 ampere.