Answer:
a.
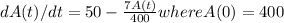
b.
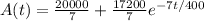
c. 3.717 kg
Explanation:
a) Write the differential equation that represents the problem.
Let A(t) be the amount of dissolved oxygen in the tank at any time, t.
The net flow rate dA(t)/dt = mass flow in - mass flow out
Since 10 g/l of oxygen flows in at a rate of 5 l/min, the mass flow in is 10 g/l × 5 l/min = 50 g/min
Since A(t) is the amount of oxygen present in the tank at time, t, and the volume of the tank is 400 liters. The concentration of oxygen in the tank is thus A(t)/400 g/l.
Also, water is being pumped out at a rate of 7 l/min. So, the mass flow out is thus concentration × flow rate out = A(t)/400 g/l × 7 l/min = 7A(t)/400 g/min
So, dA(t)/dt = mass flow in - mass flow out
dA(t)/dt = 50 - 7A(t)/400 with A(0) = 400 l × 1 g/l = 400 g since the tank initially contains 1 g/l of dissolved oxygen and has a volume of 400 l
So, the differential equation is
dA(t)/dt = 50 - 7A(t)/400 where A(0) = 400 g
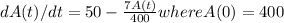
b) Solve the differential equation
To solve the equation, we use separation of variables, so
dA(t)/dt = 50 - 7A(t)/400 where A(0) = 400 g
dA(t)/(50 - 7A(t)/400) = dt
Integrating both sides, we have
∫dA(t)/(50 - 7A(t)/400) = ∫dt
-7/400 ÷ -7/400∫dA(t)/(50 - 7A(t)/400) = ∫dt
1/ (-7/400)∫-7/400dA(t)/(50 - 7A(t)/400) = ∫dt
(-400/7)㏑(50 - 7A(t)/400) = t + C
㏑(50 - 7A(t)/400) = -7t/400 + (-7/400)C
㏑(50 - 7A(t)/400) = -7t/400 + C' (C' = (-7/400)C)
taking exponents of both sides, we have
50 - 7A(t)/400 = exp[(-7t/400) + C']
50 - 7A(t)/400 = exp(-7t/400)expC'
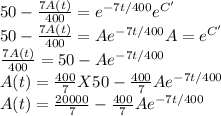
when t = 0 , A(0) = 400. So,
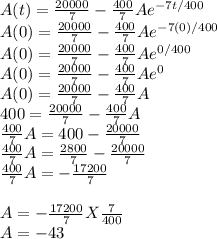
So,
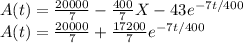
c) At 1 p.m., what is the amount of dissolve oxygen in the fish tank.
At 1 p.m, t = 60 min
So, the amount of dissolved oxygen in the fish tank is A(60)
So,
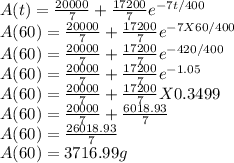
A(60) ≅ 3717 g
A(60) ≅ 3.717 kg