Question

Find the missing side length of this right triangle​

Answer 1

41

Explanation

because this triangle is a right triangle , u know that u can use pythagorean theroem to solve this.

the pythogorean theroem is
`a^(2)`+
`b^(2)`=
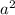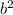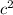`c^(2)`. the hypotenuse is the longest side or the one that the right angle is pointing to. in the equation , the hypotenuse is represented by c.

so then u juss plug in the numbers that you have so 9 sqaured + 40 squared is equal to c sqaured.

then when you simplify that you end up with 81+1600=
`c^(2)`

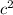
then you add the two numbers and you get 1681=
`c^(2)`

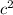
u have to get the variable by itself so you find the sqaure root of each side which would look like
`√(1681)`=
`√(c)`

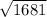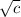
simplify that, and you get c=41

hopefully that helped ! :)